赌王为什么能赢？
上书房咨询 2020-06-01 17:22:48
北京时间5月26日，港澳知名爱国企业家、第9届至第11届全国政协常委何鸿燊在香港养和医院逝世，享年98岁。何鸿燊去世的消息传出后，港股博彩股出现异动，港股中华博彩指数盘中拉升，涨幅超过4%。赌王旗下的澳博控股涨幅一度飙高至超过8%，和何鸿燊家族相关的公司股价也出现大涨，其中信德集团涨幅扩大至超过20%，该公司重要股东之一为何鸿燊之女何超琼。
说到博彩业，受到90年代香港电影的影响，很多人会有这样的刻板印象：
所以，2020年了，还认为赌王赚钱就是在出老千吗？
其实，现代赌场有由政府发布专门的牌照，已经不是过去处于灰色地带时依靠老千、坐庄来盈利，赌场更多的是依靠数理基础来和多种业态组合来实现盈利。
电影《赌神》、《赌圣》、《赌侠》剧照
博彩产业链
博彩业和旅游业两种业态往往是互相依存，澳门的旅游产业链就是以博彩为核心拉动餐饮、购物、股票、地产、休闲娱乐等各种消费。目前，澳门已经呈现出“后博彩时代”的特征，虽然博彩业仍然是经济支柱，但是正在逐步向会展、休闲、旅游等综合项目发展。
博彩业中赌马的产业链是最长的，上游包括了繁育、饲养、训练、马匹交易，中游包括了赛事运营、赛事传播、产地租赁、俱乐部等，下游产业链包括了博彩竞技、娱乐观光、文化周边等。香港赛马会成立130多年来，既满足了市民的博彩需求，又配合港府打击非法赌博，将市民博彩的金钱引入正途。目前，香港赛马会成为香港特区单一纳税最多的机构。
随着数字经济的发展，博彩业与科技产业结合产生了新的商业模式和机会。比如中国福利彩票发行管理中心推出的视频彩票（VLT）项目，充分利用电信行业的通讯系统，实现中心机房和各地视频彩票销售厅终端的实时链接，利用网络为平台并随机产生中奖者。
庄家为什么能赢？
赌徒思维中的前后因果谬论
有一类电视节目是预测彩票号码的规律，电视上的“专家”会煞有介事的列出以往几期出现的彩票号码，并据此推测已经出现数字在下一期不会出现。这是一种典型的前后因果谬论。事实上，两次摇号的行为是独立事件，下一次号码出现的概率与上一次并没有任何关系。也就是两次出现的彩票号码都是随机的，上一次出现号码其实并不会影响下一次号码。
赌场经营基础之大数法则
在随机事件的大量重复出现中，往往呈现几乎必然的规律，这个规律就是大数定律。大数定律是指在试验不变的条件下，重复试验多次，随机事件的频率近似于它的概率。这是伯努利在1713年提出的历史上第一个极限定理，其数学含义是：当n足够大的时候，事件A出现的频率将几乎接近于其发生的概率，既频率的稳定性。
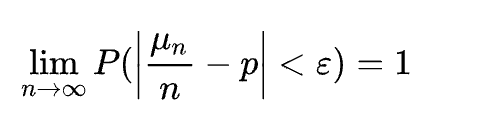
庄家不败筹码：凯利公式
在概率论中，凯利公式（也称 “凯利方程式”）是一个在期望净收益为正的独立重复赌局中，使本金的长期增长率最大化的投注策略。该公式于 1956 年由约翰·拉里·凯利（John Larry Kelly）在《贝尔系统技术期刊》中发表，可以用来计算每次游戏中应投注的资金比例。设赌客的本金为N，投注比例为f，游戏每局有n种结果，第i种结果的净收益率为ri，发生的概率为pi。则一局后对数本金 ln N 的增量（对数增长率）的数学期望为：
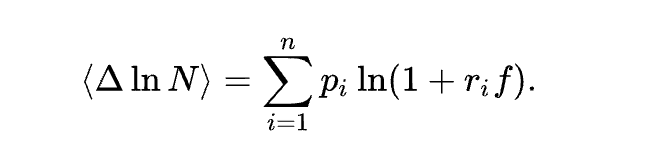
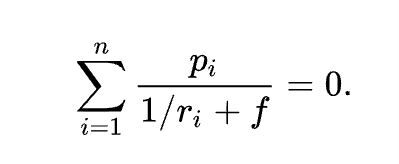
很多人说赌王运气好，但他是这样总结自己的：离不开多读书、勤力、肯牺牲。
由于家庭背景优渥，何鸿燊从小过着衣食无忧的少爷生活，就读于香港最好的学校——皇仁书院。小时候的何鸿燊不爱学习，当时成绩很差，后家道没落，何鸿燊尝尽了世态炎凉，发奋读书，以优秀的成绩考入香港大学，并获得奖学金。
由于抗战爆发，香港失守，何鸿燊于1941年香港大学理科学院肄业后，来到澳门，进入澳门联昌贸易公司工作。因一口流利的英语，他在公司担任了秘书职务。何鸿燊的记忆力非常出众，当时澳门的两千多个电话号码他能倒背如流，再加上善于交际，周旋四方，他很快成了这家公司的得力干将，并为公司立下汗马功劳。
1961年，澳葡政府规定博彩业须通过专营制度实施，何鸿燊看准时机，重返澳门，与霍英东等人合作，一举拿下赌场独家专营权，迈出“赌王”之路的第一步。20世纪90年代初，又在澳门建立“皇宫赌场”等多个赌场。除香港和澳门外，何鸿燊亦在多个国家投资，包括越南、朝鲜、菲律宾、葡萄牙等。除博彩业之外，何鸿燊的产业还涉及房地产、建筑、船务、投资等多个领域。至2011年，其旗下的企业包括：澳门博彩控股有限公司、香港新濠国际集团、香港信德集团有限公司、澳门国际机场专营公司、王牌国际、澳门诚兴银行等。
在经营理念上，何鸿燊坚持保护并推广澳门独有的中西文化，因为他相信这是澳门持续发展的优势所在，因此，他参与支持澳门各项旅游、文化、体育活动，其中包括赞助每年一度的澳门格兰披治大赛车、澳门艺术节、澳门音乐节等。
荀子曰：君子博学深谋，修身端行，以俟其时。说的就是君子要多读书、增长知识，端正品行、提高道德修养，以便等到机遇到来的时刻。赌王何鸿燊取得这样的成绩、成为澳门街的传奇，就像赌王自己总结的“离不开多读书、勤力、肯牺牲。”
作者：赵璐，经济学博士，上书房信息咨询公司合伙人，高级顾问
（本文部分图文来源于网络，如有侵权，请与我们联系及时处理）
